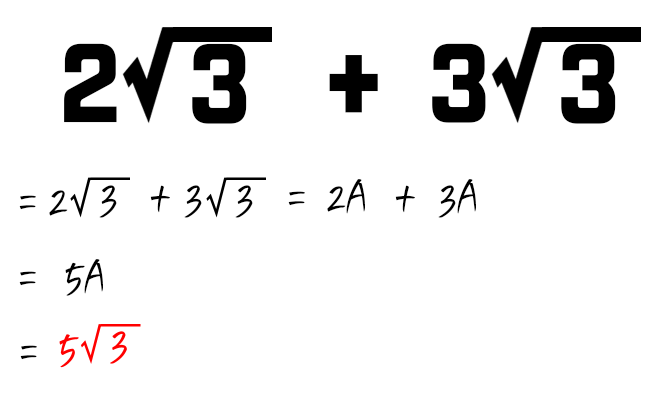
안녕하세요. 멘토 정선생님입니다.
오늘은 수학 공식에 대한 콘텐츠인데요. 루트(Root) 계산법으로 더하기, 뺄셈, 나눗셈을 한다면 어떻게 풀어야 하는지 기본 개념을 정리합니다.
수학 개념으로 불리는 루트(Root)는 제곱근의 의미와 성질에 대해 이론적인 의미를 인지해야 합니다.제곱근이란 같은 수를 두 번 곱한다는 의미를 가지고 있습니다. 구단을 한번 떠올려 봅시다. 9단의 2단에서 제곱되는 값을 찾으라면 2×2=4라는 공식을 떠올리면 됩니다.
이렇게 제곱했을 때 얻을 수 있는 숫자의 값을 그대로 표기하는 것이 아닐까요?이렇게 숫자 위에 작은 숫자로 표시하는 방식을 제곱으로 계산했다고 볼 수 있습니다. 이 표현을 수학문자로 바꿔서 표기하면 x를 a의 제곱근이라고 부를 수 있습니다.
그런데 루트 계산식에서 이 개념이 왜 필요한가? 라는 것이 핵심입니다.만약 위의 내용을 바탕으로 5의 제곱근을 구한다면 여러분은 어떻게 대답할 수 있을까요? 그렇죠. ‘5’라는 값을 제곱해서 구할 방법은 없어요.
물론 소수점마다 계산을 해서 우여곡절로 계산할 수 있지만 너무 복잡하고 시간도 걸립니다. 이럴 때 루트를 표시해서 씁니다. 다른 말로는 ‘근호’라고도 표현을 해요.
만약5제곱근을구해야한다면여러분은이렇게대답을해주셔야합니다.물론 숫자 영역에서는 음수, 양수의 개념이 있죠?그렇기 때문에 플러스 마이너스를 한꺼번에 표시하는 수학 기호 ±를 앞에 붙여 표기하면 정확한 답이라고 할 수 있습니다. 그러면 루트(Root)가 적용된 값을 더하기, 끌기, 곱하기, 나눌 때는 어떻게 계산해야 하는가가 오늘날 콘텐츠의 메인 주제입니다.
예제 문제를 보면서 기본을 쌓아볼까요?
더하기
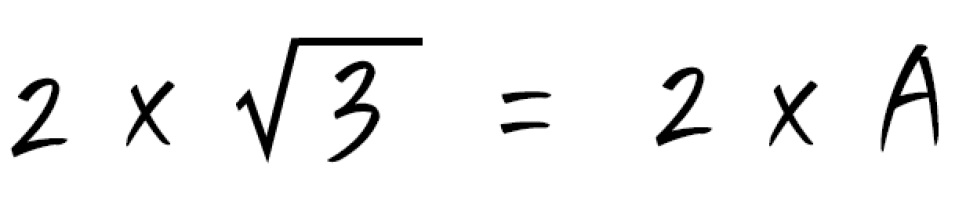
먼저 루트에서의 덧셈 방법을 알아보겠습니다. 위의 문제에서의 펙트는 어떤 것입니까?루트 값으로 묶여 있는 곳을 하나의 문자로 생각하면 됩니다. 그러면 더하기 계산은 아주 쉬워집니다.수학규칙에 자연수 값과 같은 글자로 되어 있다면 사칙연산이 된다고 배웠을텐데요? 따라서 위 문제의 정답은 이 규칙에 대해 정확히 인지하고 있으면 누구나 쉽게 풀 수 있는 내용입니다.
그래서 정답은 5×3으로 표시하시면 됩니다.빼기 루트 계산법에서 빼기를 할 때는 앞서 소개한 덧셈 때와 같은 규칙이 성립됩니다. 그런데 루트로 표시되는 값이 다른 경우는 어떻게 계산하면 좋은 것일까요?
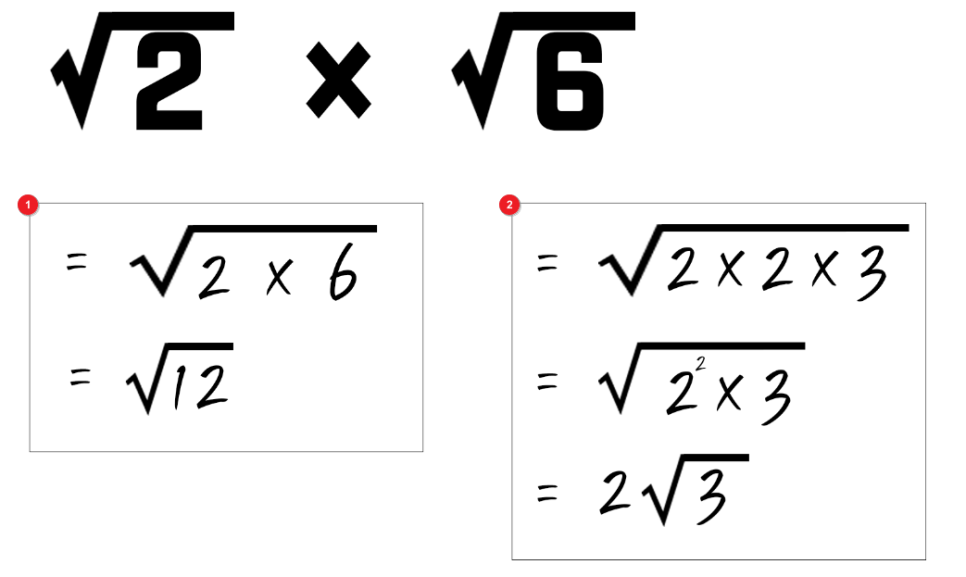
이번에는 ROOT 값이 다르기 때문에 문자로 인지한다면 서로 다른 문자로 봐야 합니다.그래서 문제 중에 정답이 있다는 말이 있듯이 문제와 정답이 동시에 나온 것과 똑같죠. 물론 위의 데이터를 계산할 수 있는 방법이 전혀 없는 것은 아닙니다.
빨간 글씨로 표시된 정답을 그대로 입력하셔도 되지만 앞으로 수준 높은 루트 계산법에서는 모두 계산을 해야 할 경우도 있습니다.오늘은 기본 원리만을 다루는 내용이기 때문에 앞으로 수준 높은 루트 문제는 별도로 콘텐츠로 제작하여 업로드 하겠습니다.:)
곱셈에서는 이번에는 루트 곱을 하려면 어떻게 하면 좋을지 살펴봅시다.앞에서 설명한 예제 문제 중에서도 등장했어요. 힌트를 드리자면 자연수와 문자로 표기했을 때 설명 문맥을 이해하시면 되겠네요.

자연수와 제곱근으로 표기할 때 눈에 보이지 않는 곱셈 기호를 생략한 값이라고 할 수 있습니다. 그런데 곱셈법은 이 내용을 보려는 것은 아니죠! 그래도 왜! 이렇게 계산하고 표기를 하는지 이유를 알아야 하는 것이 루트 곱셈법의 가장 중요한 포인트죠?
예제 문제를 보면서 원리를 이해하도록 하겠습니다.

루트로 곱셈을 할 때는 원래 제곱근 개념으로 근호가 씌운 형태이므로 숫자끼리 곱셈을 하면 됩니다. 따라서 위 문제의 정답은 아주 쉽게 계산할 수 있겠죠?
그런데 만약 아래 문제가 나왔을 때는 어떻게 계산해야 하는지 살펴보겠습니다.

계산 방정식 ①번, ②중에서 어떤 계산법이 맞을까요? 정답은②번 푸는 방법으로 계산을 하는 것이 맞습니다.처음에 제곱근에 대한 개념을 말씀드렸죠? 루트6는 2×3 형태로 해식을 만들 수 있는데, 문제로 볼 때 루트2의 값과 루트6의 값을 곱한다고 했을 때를 풀어 표현하면 이렇게 정리할 수 있습니다. 그런데 이때 ‘2’라는 숫자가 두 번 반복되었기 때문에 제곱이 되는 값은 루트 밖으로 나옵니다.따라서 최종 정답이 표기된 ②번 방식의 내용이 적절해지는 것입니다.:) 나눗셈 루트 계산법에서는 곱셈과 나눗셈에서 주의할 점이 많이 생깁니다.마지막 사칙 연산으로 루트 나누기를 할 때는 어떻게 해야 하는지 알아보겠습니다! 나눗셈에서는 역수의 개념과 약분의 개념을 익혀야 합니다.
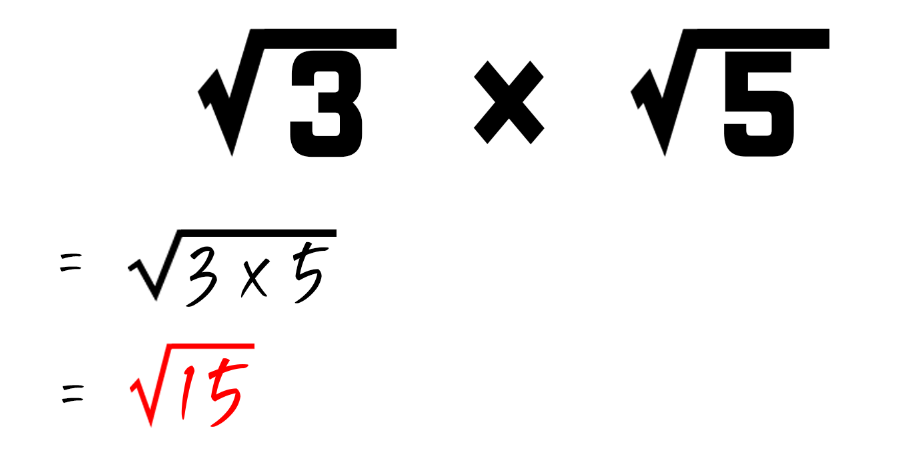
아까 걸 때 예제 문제를 나누는 것으로 바꾸고 값을 구하면 위의 사진과 같이 계산을 하게 됩니다.나눗셈을 곱셈으로 바꾸는 것! 역수의 개념이 적용된 사례이고, 이 상태에서 2와 6은 서로 약분 관계의 숫자이기 때문에 거기에 맞춰서 풀면 됩니다.
푸는 방법을 보면 어떻게 해야 할지 대충 닫힙니다.:) 오늘 소개해드릴 루트 계산법은 기초 속의 기초 내용입니다. 앞으로 푸는 방법에 관한 내용으로 종종 인사드리겠지만 그때마다 수준 높은 수학 문제를 가져오니까 그때도 같이 배우면서 공부해보시면 좋겠네요!
그럼 이만 끝내겠습니다.다음 시간에도 유익한 뉴스로 찾아뵙겠습니다. 감사합니다。